問題(Output)を解くためには、少なからず暗記(Input)しなければならない項目があります。 暗記するべきものはできるだけ少なく、あとは自ら考え方(論理)で解答を導き出せるのが理想ですが、この論理を身に着けるのには、まず理解が必要です。 その理解の確認のために問題を解く訓練をします。 訓練をすればするほど、暗記するべきものは少なくなり、応用もでき、早く解けるようになります。 理解が不十分だと、暗記すべき項目は増え、最悪、丸暗記という事態になります。 特に1アマ試験の場合、計算問題がありますのでそれにも限界があります。 しかし、ほんのちょっとしたことを知っているだけで、理解が進み、暗記すべきことが少なくなる場合があります。 ここでは、他ではあまり書かれていないアプローチで1アマ試験に必要な計算公式について解説してみました。
無線工学
物理量の単位と公式
無線工学では様々な物理量(変数)が出てきます。 これらの物理量には単位がすべて付いています。 計算問題またはこれら物理量の関係(比例、反比例、二乗に比例、etc)を問う問題は、公式を知っておればすぐに解けます。 しかし、試験本番で公式の記憶があやふやな場合、またはど忘れしてしまった場合、その解決の一助になる方法があります。 それは、公式に表れてくる物理量の単位です。 公式の中で使用される物理量に付いている単位を知っておれば、公式を思い出す助けになります。 特に、計算に使用する物理量は問題文の中で単位付きで記されていることが多いのです。
公式と単位
理系でなくても、単位は公式と密接なかかわりがあることは義務教育受けた方なら知っているはずです。 小学校で習う例でいうと
V: 速さ [m/sec] = d: 距離 [m] ÷ t: 時間 [sec]
まさに、速さ V の単位 [m/sec] が この公式 \(V = \cfrac{d}{t}\) を示しているのです。
つまり、公式とは左辺と右辺が等しいというものですから、当然単位も左辺と右辺が等しくなければならないのです。 これが不等式であっても同じです。 単位の違うものは大小を比較できないので当然です。 「1[kg]と1[m] はどちらが大きいか?」 と比較できないのです。
オームの法則
いきなり、少し難しくなりますが、すべての物理量の単位は基本的に4つの物理量単位 長さ・質量・時間・電流 で表すことができます。※1 特に、長さをメートル[m], 質量をキログラム[kg], 時間を秒[sec], ,電流をアンペア[A] で表したとき、頭文字をとってMKSA単位と呼びます。 MKSA単位は国際単位系(SI)です。 これ以外に、長さをセンチメートル[cm], 質量をグラム[g]を基準としたcgs単位系もあります。
たとえば、電気抵抗オーム[Ω] は \([\cfrac{kg・m^2}{sec^3・A^2}]\) です。
電圧ボルト[V] は \([\cfrac{kg・m^2}{sec^3・A}]\) です。
従ってオームの法則 \(E [V] = I [A]・R [Ω] \)を 4つの(SI基本)単位で示しますと
\(E [\cfrac{kg・m^2}{sec^3・A}] = I[\cancel{A}]・R[\cfrac{kg・m^2}{sec^3・A^\cancel 2}]\) で左右の単位は一致しているのです。
つまり、電気抵抗と電圧の単位をMKSAの基本単位で表せば、自然とオームの法則が導き出せるのです。 これは、先の速さを求めるの計算式と同じです。
しかし、電気抵抗の単位を\([\cfrac{kg・m^2}{sec^3・A^2}]\)、電圧の単位を\([\cfrac{kg・m^2}{sec^3・A}]\) で表すのは複雑すぎます。
そこでそれぞれ、ボルト[V]とオーム[Ω]という単位を使うことになったのです。 これらは組み立て単位と呼ばれています。 表記は楽になったのですが、その代わり、単位からオームの法則は簡単に導きだせなくなりました。
次元解析
厳密には、ここで言う、長さ・質量・時間・電流は単位というのではなく次元と呼ばれ、それぞれL・M・T・I という記号で表されます。 つまり、すべての物理量は4つの次元で表すことができるというのが正確な表現です。 この記法で表現すると、電気抵抗はML2T-3I-2となります。 上で示しましたように、物理量の次元(単位)から、複数の物理量の間の関係を予測できます。 これを次元解析といいます。 つまり、既知の物理量を組み合わせて、求める物理量の次元となるように式を作れば正しい関係である可能性が高いのです。
次元解析は、複雑な物理量が絡まった問題に対して、相互間の量の関係を推測できるのに利用されています。 まぁ、少なくとも左右の式の次元が合わない方程式は、自己矛盾していて、間違っていることが明白なわけです。
国際単位で現在決められている次元は、長さ(L)・質量(M)・時間(T)・電流(I)以外に、熱力学温度(Θ)・物質量(N)・光度(J)があり合計7つあります。 無線工学では残りの3つは使用しませんので割愛しています。 7つの次元の単位は特に基本単位(メートル・キログラム・秒・アンペア・ケルビン・モル・カンデラ)と呼ばれています。 国際単位は、真空中の光の速さ・電気素量・プランク定数・… などの同じく7つ定義定数を固定することで7つの基本単位が導き出されます。 基本単位に対して、ラジアン・オーム・ジーメンス・ボルト・ワット・ヘルツ・ヘンリー・テスラ・ウェーバ・クーロン・ファラッド・… などはSI組立単位(22個ある。)として、利便性のの観点から個有の名称と記号が与えられています。
1アマ試験における次元解析の例
平面大地上の電界強度
下記の電界強度を計算する式は、これまでの試験で問題文中に与えられていましたが、今後与えられるという保証はありません。
\(d\gg h_1,\qquad d\gg h_2\) の条件では、
$$ E=E_0 \cfrac{4\pi h_1 h_2}{\lambda d} \tag{1} $$
\(E\): 直接波と反射波の合成電界強度[V/m]
\(E_0\): 直接波の電界強度[V/m]
\(\lambda\): 波長[m]
\(d\): 送受信点間の距離[m]
\(h_1, h_2\): 送信、受信アンテナの地上高[m]
この式で、左右の辺にある\(E\)と\(E_0\)は電界強度で単位は等しいです。 従いまして、右辺の残りの\(\cfrac{4\pi h_1 h_2}{\lambda d} \tag{1}\)のは無次元でなければならず、そのためには分母と分子の単位が等しくなければなりません。
また、電界強度がアンテナ高\(h_1, h_2\)(単位[m])に比例し、距離\(d\)(単位[m])に反比例するのは直感的に分かります。
波長\(\lambda\)(単位[m])はどうでしょうか? 迷ったときに、左右の次元が等しくなるためには分母にくるべきだと分かります。
相対利得Gのアンテナの電界強度E[V/m]
1アマの試験では下記の式は記憶することがほぼ必須です。
$$E=\cfrac{7\sqrt{GP}}{d} \tag{2} $$
\(G\): アンテナの相対利得[倍率]
\(P\): アンテナの放射電力[W]
\(d\): アンテナからの距離[m]
左辺は電界強度 E [V/m] です。
右辺は \(d\) 距離[m]で除していますので、\(7\sqrt{GP}\) の部分が電圧の単位 [V]です。
\(G\)は[倍率]なので、無次元です。\(P\)の単位は、[W]です。
ここで、電力[W] = 電圧[V]*電流[A] = \(\cfrac{(電圧[V])^2}{抵抗[Ω]}\)
したがって、\(\sqrt{GP}\) の単位は [V/\(\sqrt{Ω}\)]です。
\(\sqrt{Ω}\)の単位は定数7が持っています。 これを導き出すには次の電力束密度と電力束密度から電界強度への換算式の理解が必要です。
距離Rの位置の電力束密度Sを計算する式
電力束密度S\([W/m^2]\)は、単位面積当たりの電波の電力です。
アンテナから放射される電力束密度 S\([W/m^2]\) は、電力PGa[W]を半径R[m]の球の表面積(\(4\pi R^2\))で除した面密度に換算した式なので、直感的に理解できると思います。 つまり、球の中心1点から等方向に放射されたエネルギーは、半径Rまで広がったとき、その表面のすべてを集めたものに等しいというエネルギー保存則です。 この時のアンテナはダイポールではなく、等方アンテナです。
$$ S=\cfrac{PGa}{4\pi R^2} [W/m^2] \tag{3} $$
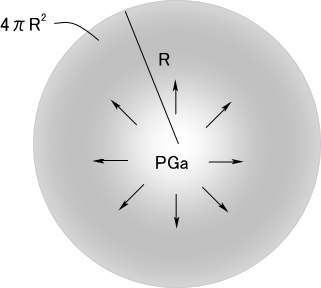
S: 電力束密度 \([W/m^2]\)
Ga: 絶対利得[倍率]
R: 距離[m]
P: 入力電力[W]
電界強度Eから電力束密度Sへの換算
電波は電場\(\vec E\)と磁場\(\vec H\)が交互に相互作用しながら空間を伝わるエネルギーですから
$$ \vec S=\vec E\times\vec H=\vec E\times\cfrac{\vec E}{120\pi} \tag{4} $$
$$ \vec S=\cfrac{E^2}{377} [W/m^2] \tag{5} $$
\(120\pi\)は真空自由空間のインピーダンス[Ω] で. \(Z_0 = \sqrt{μ / ε} = \sqrt{μ_0 / ε_0}\) = \(120\pi\) です。
\(μ_0\): 真空の透磁率
\(ε_0\): 真空の誘電率
なお、真空中の光速度\(c\) = 299,792,458 [m/s]と以下のような関係があります。
$$ ε_0=\cfrac{1}{μ_0 c^2}= \cfrac{1}{Z_0 c} $$
半波長ダイポールアンテナの電界強度Eを求める
(3)式と(4)式から
$$ \cfrac{E^2}{120\pi} = \cfrac{PGa}{4\pi R^2} $$
$$ E = \sqrt{120\pi\cfrac{PGa}{4\pi R^2}} $$
$$ E = \cfrac{\sqrt{30・PGa}}{R} $$
半波長ダイポールアンテナの絶対利得 G =1.64*Ga を使うと
$$ E = \cfrac{\sqrt{30・1.64}\sqrt{PG}}{R} = \cfrac{\sqrt{49.2}\sqrt{PG}}{R} ≒\cfrac{7\sqrt{PG}}{R} \tag{6}$$
つまり、7の単位は自由空間インピーダンス[Ω]の単位の平方根から由来します。
このように難しい理屈は抜きにして次元だけに注目しても関連する式がすべて芋ずる式に導出できるわけです。


