選択肢問題を解くときのテクニック
第一感でマーク付け
以下のテクニックは、1アマの試験に限らず選択肢問題を解くときの一般的なテクニックです。 今や学校のテスト以外、マークシートの試験は珍しくないので当たり前のテクニックですが、以外と実践していない人が多いので、敢えて記載しました。
選択肢を読んだとき、正しいのか間違っているのか第一感をマークします。正しければ○、間違っていれば✖️、正しいと思うが自信がないは△、成否が全くわからないは?、等々です。マークは自分にとってわかりやすい方法でつけてください。
このようにしておくと、正しいものを選択するのか、間違っているものを選択するのか、すべての選択肢にマークがついたとき問題文の前提を読まなくても、明らかになります。 ※ほとんどの選択肢が?や△ではダメですが^_^; ダブルチェックになります。
マークとして番号やアルファベットを使うのはやめた方が良いでしょう。 特にマークシートの場合は選択肢を番号で塗りつぶすものが多いので転記するときに、マークである番号と解答すべき選択肢の番号を間違うことがあります。
私の場合、穴埋めを選択肢から選ぶ 法規のB-2問題 で誤答しました。マークシートに転記する時、解答の内容である数値と解答の選択肢番号を取り違えたのです。
2020年秋期 1アマ 法規 問題B-2 の一部
アマチュア無線局における周波数測定装置の備え付けが必要の無い送信装置は
空中線電力[ ]以下のもの
正解の選択肢の番号は 3. 10ワット でしたが、慌て者の私は、解答の内容である 10 をマークしてしまいました。 したがって穴埋めのところに書き込む場合、解答の内容を書くのではなく必ず選択肢番号を書くように習慣づけてください。
問題文をよく読む
あらゆる試験の基本中の基本なのですが、これもまた実行していない方が比較的多いのです。 まず、問題文を2度読みする。 鉛筆でなぞりながら読むと読み落としが少なくなります。 そこには、問題文は正答として何を求めているのか必ず最初に書いてあります。 選択肢の中から正しいものを1つ選ぶのか、間違ったものを1つ選ぶのか確認しましょう。 それには、選択肢の文を読む前に何を求めているのか該当部分にアンダーラインを引いて強調しておきましょう。 また、計算問題でも、たとえば、回路全体の電流や電圧を求めているのではなく特定の素子の電流や電圧の値を要求している場合がありますので注意しましょう。
値を選択する場合でも、「正しいもの」を選ぶのか「最も近いもの」を選ぶのか問題文の言い回しが異なることがあります。 それが、正解値を求める上でのヒントになることがあります。 問題集を解いているとき「あれ、解答欄に計算結果がない…」しかしよくよく見ると求められているものが違ったという経験もあるでしょう。 この時、もし、回答欄に誤った計算結果と合致する選択肢が偶然?あれば間違ってしまいます。 計算問題の場合、「正しいもの」を求められている場合は、計算結果が割り切れるはずであり、「最も近いもの」を求められている場合は、端数が残るというヒントを利用しましょう。
1アマ試験の問題は、あまりひねくれた問題は無いようです。しかし、軽いひっかけ問題がごくわずかですが混ざっています。 過去問で何度か出された問題でマンネリ化しているような出題にたまに見られます。 「この問題見た事ある!」と飛びついて急いで回答するのは良くありません。 慎重に解くと正答できる問題であるのだからこそ、間違うと痛いです。
2020年秋期 1アマ 法規 問題A-15
次のモールス符号の組合わせのうち、「そちらの伝送は、かなりの混信を受けています。」を示すQ符号を表したものはどれか。下の1から4までのうちから一つ選べ。
1 --・- ・-・ -・ ・・---
2 --・- ・-・ -- ・・・--
3 --・- ・-・ -・ ・・・・-
4 --・- ・-・ -- ・・・・・
私は、慌てて4を選択して間違えました。 「かなりの混信」ですから QRM 3 です。 従って正解は、2です。 引っかけ問題と言うより私の不注意に近いミスですが…
その他
1アマの試験問題は、国家試験の中でも比較的素直な問題が多い方です。 特に項目5.以降は、それでも迷ったときの私の指針です。
- 解答欄を間違わないように記入する。
- 易しい問題から解く。
- 取りかかった問題が難しくてすぐに解けそうにないときは、こだわらず別の問題に進む。
- 一つだけ(正しいかそうでないか)異なった肢を選ぶときは、その問題の本質を見て判断する。
- 2肢のどちらかが正解か迷ったときは、曖昧な知識や記憶に頼らず、目的とする趣旨を考えて判断する。 2つ肢の中で違いを問うていることが多いのでその違いが生ずる理由を考える。
- 「必ず・・・である」は誤りが多い。 法令の場合、例外がつきものです。「必ず・・・である」とか「・・・に限られている」という言葉場は例外がないという意味であるから、誤りであることが多い。
- 見慣れない、難解な選択肢は答えに無関係であることが多い。 出題者は選択肢を増やすため、惑わすような難しい肢を入れることがある。
法規の問題を解くコツ
私は、いくつかの国家試験を受けてきましたがアマチュア無線に限らず法的資格を伴うものは必ず法規の問題があります。 ※私が合格したのは宅地建物取引士と社会保険労務士です。 そのほか、情報処理1種もありますがこれは法的資格を与える試験ではなく法規の問題はありません。
以下は、法学概論ではありません。あくまで、1アマレベルの法規問題を解くための考え方です。 従いまして、用語等は厳密な法律用語を使用していません。 自動車運転免許証をお持ちの方なら、ペーパー試験のときのことを思い出して下さい。
法律の問題といえば、条文の暗記しかないというのが定番ですが、1アマの試験は、比較的厳密な知識を求められるのではなく、大まかな趣意を理解しておれば正解できます。 ただし、キーワードに関しては正確に覚えなくてはなりません。 そのためには、法規の問題を解く上で重要な考え方があります。 それは法の精神です。 法律の趣意とか趣旨とも言います。 その法律ができた背景を理解すれば、たとえ細かい条文の内容を知らなくてもある程度正解は導き出せるのです。
無線従事者の免許や無線局の免許は何のためにあるのでしょう。 法的資格とは法律で規制されている行為でも、その資格を持っていれば法律違反にならないものをいいます。 つまり、規制の対象となる行為はデフォルト(無資格・無届け・無許可)では禁止なのです。
法律はまず最初にその法律がつくられた目的を示し、次に言葉の定義、禁止されている範囲、それをすることが許される範囲と資格、罰則の順に記されています。 手続きや形式なども書かれていることもありますが、細かいことは政令(施行令)・省令(施行規則)で定めるということになっています。
電波法では第1条に
「この法律は、電波の公平且つ能率的な利用を確保することによって公共の福祉を増進することを目的とする。」と書かれています。
たとえば、過去問によく出る内容として、正誤を問う問題で
「無線局を運用する場合においては、空中線電力は、免許状に記載されたところによらねばならない。ただし、遭難通信については、この限りでない。」
というのがありますが、正しいとするなら1kW出力で免許されている局はいつも1kWで送信しなければならなくなります。 これは明らかに(第1条の目的)電波の公平且つ能率的な利用に反しています。 従って間違いです。 正しくは、「電波法 第54条 空中線電力は免許状に記載されたものの範囲内で、通信を行うため必要最低であること。」ですが別に知らなくても第1条の目的を理解しておれば判断できる内容です。
無線工学(特に計算問題)を解くときのコツ
理系出身者でも填まりやすいところ
基本的に理系出身の方で、まじめに物理・数学・電気工学等の履修された方は、1アマの無線工学試験は少し勉強すればクリアできるのではないかと思いがちですが、高をくくっていると落とし穴がいくつかあります。 私自身、原子力工学科出身で、しかも社会人になってからも、数学を駆使して? 多くの分野の科学技術計算に携わり、現在、電磁場解析ソフトウェアを開発している技術者ですが、いくつか填まりやすいところがありました。
つまり、試験と実践とは以下の点で異なります。
実践では考える時間は試験より遙かに多くあり、調べ物はPCや電卓はもちろんのことインターネットや書籍を使ってもかまいません。 また、シミュレーションソフトを使うこともできます。 ただし、絶対に間違ってはいけません。 満点に近い出来が要求されます。
試験では、少なくとも1問数分で解かなければなりません。 1アマの無線工学の試験は30問、単純計算して、150分で一問平均5分です。 ただし、計算問題は10問程度で、時間が少しかかるのは数問です。 また、試験では、間違っても怒られませんし、合格ラインの正答率が得られれば良いのです。 計算問題の解答は選択肢の中から選べます。 計算がとんちんかんだと選択肢にない結果が出ますので間違いであることに気づきます。 また、全く計算が合わなくても択一問題なので、最悪の場合、それらしい肢を選択すると当たることもあります。 大抵は不正解ですが^_^:
特に理系で物理と数学に強い方は、公式なんか自分の知っているものだけで十分だと考え、後は導き出せると思いがちですが、1アマの試験で問われるのは、基本、工学なので具体的な数値で計算します。 数学の式の変形などないと言っていいでしょう。 その分や易しいのですが、たとえば、単純なオームの法則でも、4桁のかけ算や割り算をするとミスすることがあります。 電卓が使えない状態で桁数の多い数値の手計算を何段も重ねて計算するのは時間がかかり、途中で計算間違いをしてしまいます。 折角理解できている問題をくだらないミスで落とすことになります。
つまり、解き方は知っていても、簡単に解く方法や公式に明るくないとNGなんです。 卑近な例で言うと、二次方程式や三次方程式を解くとき、簡単に解を求めることができる場合に根の公式を使うのは非効率です。 特に、1アマの計算問題は、一見複雑な計算が必要に見えても、適切な公式を使えば、簡単に解けるようになっています。 端数についても基本的にはきれいに消えます。 消えない場合は近似値を求める問題(問題文が近いものを選ぶようにと書かれている)以外は、まず、間違っていると考えて良いでしょう。 時間に余裕がないときは、概算で計算しても良いですが、実際にはきっちり計算しても時間のかかる問題はほとんどなく、計算が複雑で多くなるような場合は、解き方が適切でないと考えて下さい。 しかしながら、どうしても計算量が多くなる解き方しかできない場合は、背に腹はかえられません。 潔く、計算ミスをなくすため概算する方向に転換した方が良いです。
文系で計算が苦手な方は、まず、ひたすら公式を覚えて下さい。 今から、数学や物理の基礎から学ぶにはあまりにも時間がかかりすぎます。 文系の人が得意な記憶力とパターン認識?で解きましょう。 数多くの問題のパターンを見て、どの公式を使うのか仕分ける練習します。 さらに、問題文で与えられている数値が、公式のどの変数に相当するのか見極められるようにして下さい。 最初に理論を理解する方法をとるより、覚えるのがかなり辛くなりますが、公式の意味を無理して理解しようとせず覚えた方が早いです。 1アマの計算問題のいくつかは、お決まりのバターンで解けますので、このような方法でも合格圏内には入るでしょう。 今年(2020年)秋期の試験に限って言えば、無線工学A-1の問題で簡単なベクトルの加算の演算があったくらいで、それ以外の計算問題はすべて中学生レベルの数学力で計算できるものでした。 試験においては、理論を理解しておれば、単に間違えることが少なく覚えやすい(忘れても思い出せる)というだけです。
インピーダンスの計算は本当に必要か?
無線工学ではとかくインピーダンスに関する計算が出てきます。 特に、交流回路の計算問題は必ず出ます。 インピーダンスの計算するときでも、複素数計算を使えば必ず解けますが、まともに計算すると時間がかかってしまう場合があります。 私は、複素数より複雑な四元数(quaternion)の計算もできますが、それはそれ、複素数計算をゴリゴリするのは試験向きではありません。 試験では、まず本当にインピーダンスの計算が必要か考えなければなりません。 たとえば、インピーダンスを計算しなくても、交流回路の電流は、単純に各素子の電流の自乗和の平方根で計算できる場合が多いのです。
インピーダンスの計算が必要な問題
数は少ないですがインピーダンスの計算が必要な問題もあります。 選択肢が複素数になっている場合、インピーダンスを計算(複素数計算)する必要があるでしょう。
キルヒホッフの法則とミルマンの定理
同じようにキルヒホッフの法則があります。 キルヒホッフの法則は万能ですが、変数が多くなり通常は多元の連立一次方程式になります。 連立一次方程式を変形して解いていく過程では、単なる数式変形が長々と続きます。 そこで計算間違いをする可能性が格段に増えます。 1アマの過去問で頻出した回路の問題でキルヒホッフの法則を使えば複雑になるが、ミルマンの定理などを使えば、簡単に解ける問題がありました。 ミルマンの定理は、一見複雑そうですが、並列の合成抵抗の式とオームの法則の拡張だと見ることができます。
ミルマンの定理
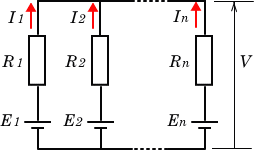
$$V=\cfrac{\cfrac{E_1}{R_1}+\cfrac{E_2}{R_2}+\cdots+\cfrac{E_n}{R_n}}{\cfrac{1}{R_1}+\cfrac{1}{R_2}+\cdots+\cfrac{1}{R_n}}$$
この式は、電圧源を短絡したとき各抵抗に流れる(短絡)電流の和を \(I\) とすると、
$$
I = \sum_{i}{}I_i= \cfrac{E_i}{R_i}
$$
です。 また、列の合成抵抗 \(R\)とすると
$$R = \cfrac{1}{\sum \cfrac{1}{R_i}}$$
ですから、ミルマンの定理は
$$V=I\times R$$
つまり、
端子電圧 = (短絡)電流 \(\times\) 合成抵抗
というオームの法則の式そのものになります。 ただし、短絡電流はミルマンの定理をオームの法則の拡張と見立てて仮想的に考えた電流であって、実際に各抵抗に流れる電流ではありませんので注意して下さい。 たとえば抵抗\(R_1\)に流れる短絡電流は\(\cfrac{E_1}{R_1}\)ですが実際に流れる電流は\(\cfrac{V-E_1}{R_1}\)です。 また、ミルマンの定理は交流でも成り立ちます。 これを全電流の定理とも言います。 交流では各抵抗\(R_i\)に相当する部分がインピーダンス\(Z_i\)に置き換えられるだけです。
同じような電源と抵抗の並列回路でも、問題設定で与えられた値から(特に電流値が与えられると簡単に解ける場合が多い)ミルマンの定理やキルヒホッフの法則を使うまでもなく、単純なオームの法則だけで解ける場合もありますので、回路図を見ただけで判断せず、問題文をよく読んでもっとも簡単な方法で解いて下さい。
数値計算は最後まで保留しておく、途中で丸めない
公式を使って解くときはなるべく簡単な式で解ける方法を選ぶことはもちろんですが、求める数値を出すまで、具体的な計算は保留しておくべきです。 なぜならほとんどの場合、1アマの試験問題では、最終的な数値を計算するとき、分母分子で互いに打ち消しあったり、平方根を計算しやすい値になったりするからです。
さらに、問題文由来の数値を途中で丸めずそのまま使って計算式を立て計算することです。
その理由は、あとから検算するとき、この数値はどこから来たのか簡単にチェックできるからです。 丸めてしまっては、その数値の由来が分からなくなり、検算のとき、どこで間違ったかわかりにくいのです。 転記量は増えますが、その分、後からの検算が楽になります。 問題用紙の裏側は白紙ですので計算スペースとして十分広いです。
複素数計算で有理化はなるべく最後にする
複素数の計算の場合でも、複素数が分母に来たときすぐに有理化するのではなく最後にして下さい。
たとえば、\(\cfrac{3}{1+j2}\) を有理化すれば
$$\cfrac{3}{1+j2} = \cfrac{3}{1+j2}\times \cfrac{1-j2}{1-j2} = \cfrac{3(1-j2)}{1-(j2)^2} =\cfrac{3-j6}{5}$$
ですが、別のファクタで \(4+j8\) が乗じられたとき、有理化していなければ、すぐに
$$\cfrac{3}{1+j2}\times (4+j8) =\cfrac{3}{\cancel{1+j2}}\times 4(\cancel{1+j2}) =12$$
と分かりますが、有理化してしまっては、
$$\cfrac{3-j6}{5}\times (4+j8)$$
の計算が必要になり面倒です。
平方根もそのままで
\(\sqrt{8}\)も \(2\sqrt{2}\) にするのではなく\(\sqrt{8}\)のままが良いです。
もちろん\(\cfrac{1}{\sqrt{2}}\) を \(\cfrac{\sqrt{2}}{2}\)にしてはいけません。 複雑になるだけです。
最後の計算まで持ち越して最終的に簡単にしましょう。
補助単位の計算は記号のまま扱う
補助単位の \(m, k, \mu, M, n, G, p\) はその記号のまま計算しましょう。 \(10^6\) とか指数にすると間違います。 指数計算が必要なとき、最後に指数にします。 \(m と k、\muとM、nと G\) は互いに打ち消し合うのを利用します。 \(k^2 = M、m^2 = \mu、\mu^2 = p \)もよく使います。 問題の選択肢によっては、指数の計算が要らない場合があります。 抵抗値が \(kΩ\) で電流値が\(mA\)の組み合わせは試験でも実際の回路でもよく出てきます。 降下電圧は互いに補助単位が打ち消し合い\(V\)になります。 ただし、最終的に解を求めるとき平方根が混じっているときは指数が奇数の場合注意です。 \(\sqrt{100}=\sqrt{10^2}=10\)や\(\sqrt{10000}=\sqrt{10^4}=100\)ですが、\(\sqrt{10}=\sqrt{10^1}≒3.16\)や \(\sqrt{1000}=\sqrt{10^3}≒31.6\)です。 また、\(\sqrt{10}≒3.16\)は円周率\(\pi ≒ 3.14\)にかなり近い値であることも心の片隅に覚えておいて下さい。
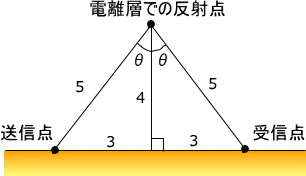
電波伝搬の問題で頻出する辺の比が 3:4:5 の直角三角形
電離層で反射される最高使用可能周波数(MUF): \(f_M\)[MHz] のセカント法則があります。
$$f_M = f_c \sec \theta$$
\(f_M:\) 最高使用可能周波数(MUF) [MHz]
\(f_c:\) 電離層の臨界周波数(MUF) [MHz]
\(\theta:\) 電波の電離層への入射角
送信点と受信点と反射点を結んだ三角形の計算で、辺の比が 3:4:5 または 4:3:5 の直角三角形(斜辺が5で他の2辺が3と4)が問題によく出ます。
この三角形は三角定規で使う辺の比が \(1:1:\sqrt2\) または \(1:\sqrt3:2\) の直角三角形と違い、角度\(\theta\)が中途半端な値ですが辺の比はすへて整数(三角定規は無理数が混ざる)です。
中学生レベルの幾何学ですがよく出ます。 なお、辺の比がすべて整数で内角もすべて整数(度単位)なのは正三角形しかありません。 しかし、正三角形の場合、高さが無理数になるため、面積も無理数になります。
もちろん、辺の比はピタゴラスの定理から簡単に計算できますが、3:4:5 の直角三角形の辺の比くらいは反射的に出るようにしても損はないでしょう。 ただし、角度は直角以外、中途半端になるということは覚えておいてください。
学習計画を立てよう
学習に必要な期間は、既にお持ちの知識と資格によって大きく異なると思います。 しかしながら、1アマの試験は年3回、4ヶ月ごとに実施されますので(今年はコロナ過で4月の試験が中止になり、8月の試験は9月にずれ込みましたが)、4ヶ月~2ヶ月程度だと思います。
私の場合は、40年くらい前に電話級(今で言う4アマ)をとって、それから開局もせず、今年(2020年)7月になってから1アマの受験を思い立ち、問題集が届いて、学習を始めたのは7月10日からでしたから、試験の日までおよそ70日ありました。 試験のため購入した書籍の詳しい内容は、別の投稿1アマ受験問題集と参考書で説明しています。
学習範囲とレベルの調査
まず、最初にどのような範囲の問題がどの位のレベルで、またどのくらいの量で出題されてるのか知るために「やさしく学ぶ 第一級アマチュア無線技士試験」を通読してみました。 計算問題はすぐに解き方が分かるかどうか、それ以外の知識を問う問題は自信を持って解答できるかどうかを判断してみる程度でしたが、以外とボリュームが多く、期間は7日間ほどかかってしまいしました。


電磁気学を本業とする私でも、無線工学の計算問題になれるまで時間がかかりそうです。 しかし、法規を含め知識を問う問題はそれほど時間がかからないことが分かりました。
習得するのに時間がかかる計算問題から
7月一杯までは、覚えるべき公式の由来などを調べながら、じっくりと無線工学の計算問題にとりかかることにしました。 計算問題は、「計算問題突破塾」を中心に進めました。 ときどき、法規の問題を息抜きに解いたりしました。 また、モールス符号やQ符号、電波形式など暗記中心の項目を洗い出し、この時期暗記カードを作りました。 初めて購入した無線機をいじったり、開局免許を申請したり、アンテナ設置したり、割とのんびりやってましたので、結果的に予定をかなりオーバして、8月中旬までかかってしまいしました。
過去問を何回転できるか


8月下旬から、過去問を解く学習に移りました。 基本は画像左の「合格精選450題試験問題集」を使用して全問を解き、次に間違ったところを解き、また、全問を解くという繰り返しを3回実行しました。 試験まであと10日というところで、「1ハム 国家試験問題集 2019/2020年版」の問題集を解きました。 問題数はこちらの方が多く、範囲も広いのですが、「合格精選450題試験問題集」をこなしておれば、かなりの早さで学習することができます。 「合格精選450題試験問題集」をこなせば十分合格すると思いますが、より確実にしたい方は「1ハム 国家試験問題集 2019/2020年版」を学習して下さい。 私のように二つとも学習する必要はないと思います。 二冊買ってしまったので使わないと勿体ないと思い学習しました。 ただ、1アマ受験問題集と参考書の投稿でも書きましたが、「1ハム 国家試験問題集 2019/2020年版」の巻末の公式と法規のまとめは学習の初期の段階でも非常に役に立ちます。
暗記カードについて

私はすでに65歳を過ぎていますので記憶力はかなり低下していますが、実は若い頃から、いわゆる丸暗記というのは苦手で暗記カードをよく利用していました。 記憶が得意な方は、カードなど作らなくても覚えられるようです。 暗記カードの良いところは、いつでもどこでも、病院の待合室でも取り出してほんの短い間でも学習できることです。 昔、暗記カードや暗記ペンなどを使用して良く覚えました。 しかし、いまはスマフォという非常に便利なツールがあります。 そこで、どのようなアプリがあるのか、3つほど試用してみました。
オススメは Ankiアプリ


私が、最終的に選択したのは、 オープンソフトウェアのAnki というアプリです。 Windows PC, Android Phone, iPhone どれでも共通してかつカードを同期して利用できる優れたアプリです。 また、モールスなどはユーザがアップロードしたカード群(Ankiではデッキという。) があり、すぐにダウンロードして利用できます。 カード反転という機能があり、カードの裏表を逆にして出題もしてくれます。 数式、画像、音声などもカードに含めることができます。 しかし次の欠点もあります。
- iPhone版のみ$24.99 で有料(この費用で開発をまかなっているらしい)
- 穴埋め問題も作れるが、効率的ではない。 特に法律の条文を覚えるには向かない。 長い文章を入力するのも大変だし、小さな画面で問題を読むのも大変。 暗記ペンを利用した方が効率的で早い。
- 作られたカードによってはその録音形式により音が再生できないデバイスがある。 私がAnkiのライブラリにあったモールス学習用の音がiPhoneで再生できませんでした。
このアプリのもっともいいところは、PCとiPhone をカードと学習履歴を同期させることができ、入力をPC側でするとカード作成が効率的にできることです。 スマフォの小さい画面でカード作成するのは非効率です。 また、学習中にカードを修正したり、追加したりすることができます。 さらに、非常にいいことは、人の忘却曲線に合わせ、かつ学習者の正答率に合わせてトレーニングを自動的に分単位でスケジュール管理してくれることです。 アプリに任せておけば、その日学習すべき内容を自動的に出題してくれます。 ユーザがすべきことは、カードを作ることと、アプリから出題される問題をこなすことです。 もちろん、直前のすべてのおさらいとか、覚えるまで日にちが少ないなど、出題を設定するモードもあります。 学習結果やあとどの何日で完璧?になるかも予想してくれます。(下記左の画像)
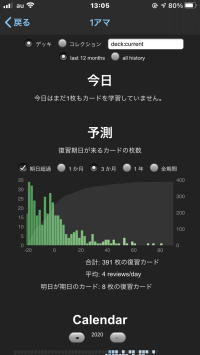
学習進捗と予測
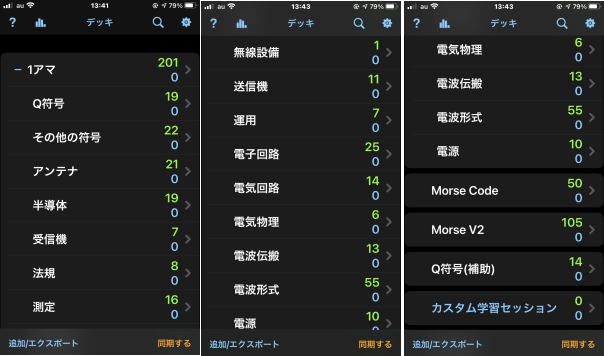
上の画像は私が作成したデッキ
無料ダウンロードできる共有デッキの中に「第一級アマチュア無線技士 国家試験 過去問」があります。 国家試験問題のそのもののデッキですので、スマフォで見るには老眼の私にとってはきついため使用しませんでした。 若い人向けにはよいでしょう。 また、問題そのものですので暗記すべき項目ではありません。 ただし、いつ消されるか分かりませんので注意して下さい。
実は、私が既に作成した1アマ受験用デッキがあるのですが、それを使えば、カードを作成する手間も入りません。 記憶の仕方などのヒントもあります。 しかしながら、自分の学習用に作成したものですので、内容に少し偏りがあり、適当に作った部分もあります。 公開したいのもやまやまなんですが、著作権の問題もありますので、そこのところ自由配布できるように、全部作り直さないといけません。 いましばらくお待ち下さい。 2020年12月期の試験には間に合わないと思いますのでご容赦下さい。


