ピタゴラスと言うと中学校で習う直角三角形の三平方の定理が有名です。 実は、この定理は相対性理論を簡単に説明したりするのに非常に便利です。
特殊相対性理論で出てくるローレンツ因子などは、ピタゴラスの定理で簡単に導出できます。
ローレンツ因子γは、\(v\)で動く宇宙船の座標系での「1秒」が、静止系からみると縮んで何秒になるかを示したものです。
宇宙船内で進行方向に対して垂直に光を出した時、1秒間に進む光の距離を、宇宙船内と外部の静止系から見た距離を比較すると簡単に、ローレンツ因子が導出できます。 下図
\((γc)^2 = c^2 + (γv)^2\)
$(γc)^2- (γv)^2= c^2 $
$γ^2(c^2 -v^2)= c^2$
$γ^2 = \cfrac{c^2}{c^2 -v^2}$
右辺の分母分子を$c^2$で割って、$γ$は時間なので$γ>0$から
$γ = \cfrac{1}{\sqrt{1 -\cfrac{v^2}{c^2}}}$
つまり、船内の1秒は、静止系から見ると$γ$秒に見え、静止系の時間が速く進む(相対的に船内の時間がゆっくり進む)ことになるのです。
・もう一つ、$E=mc^2$ のもう少し詳しく表現した
$E^2 = m_0^2c^4 + p^2c^2 $
と言う式もピタゴラスの定理で示すと下図のようになります。
なお、光は質量が0ですが、運動量となるエネルギーを持ちますので、力積=運動量 の式から光の圧力$F$が生じます。
$F・t=p$
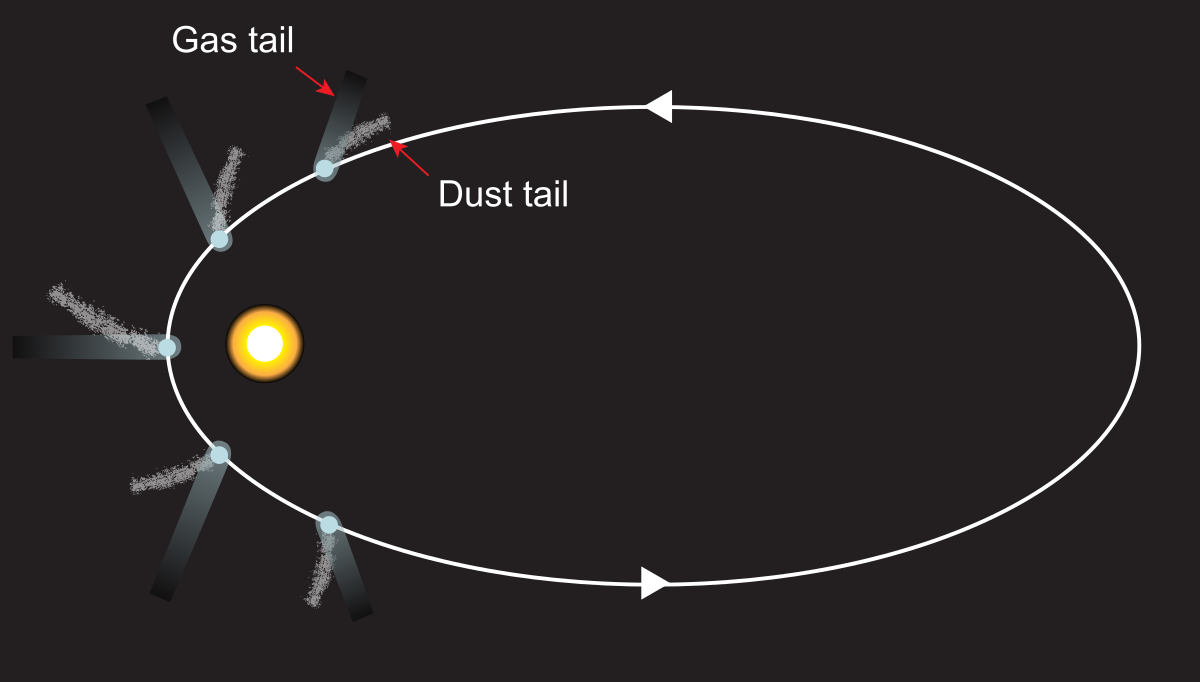
彗星の尾が太陽と反対側に流れるのは、太陽光の放射圧であると言われています。
以下 彗星の尾(Wikipediaより)
<a href=”//commons.wikimedia.org/wiki/User:%D0%AE%D0%BA%D0%B0%D1%82%D0%B0%D0%BD” title=”User:Юкатан”>Юкатан</a> – <span class=”int-own-work” lang=”ja”>投稿者自身による著作物</span>, CC 表示-継承 4.0, リンクによる


